承接自上文。本文大部分材料来自SIGMOD 19年Tamer Ozsu老师的一篇论文[2]。
图分割算法的特性罗列如下(截图自原文):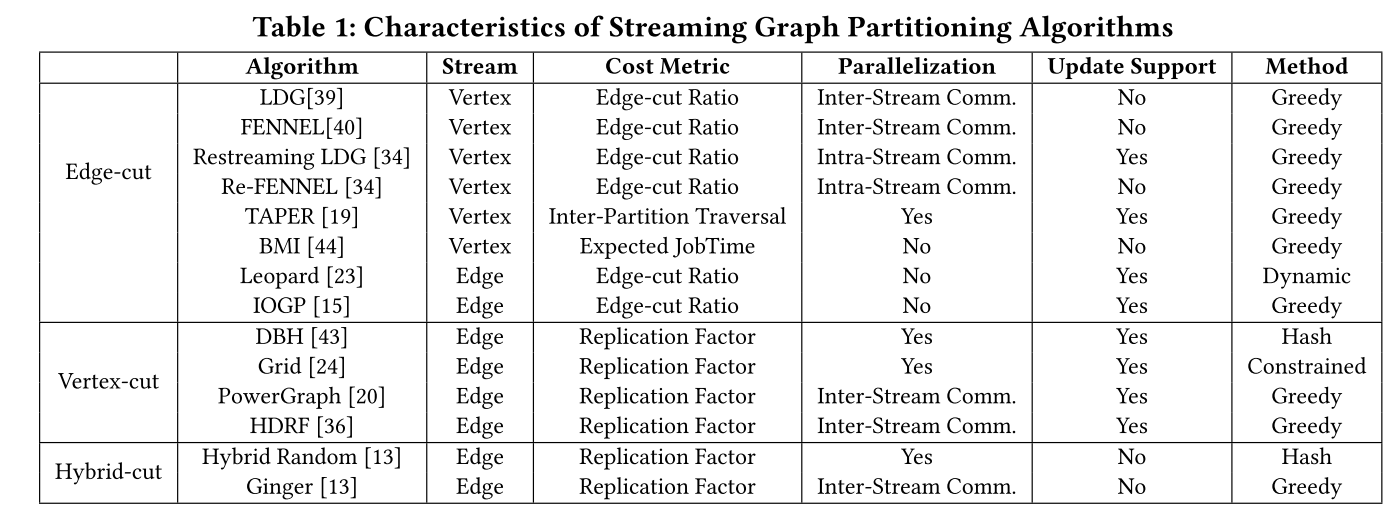
流式图分割 (SGP: Streaming Algorithms for Graph Partitioning)
流式图分割在2012年KDD的一篇文章中给出了定义[1]。有别于传统的图分割,流式图分割一次处理部分图数据,并对于拿到的部分图数据分配到各个节点当中,之后不再迁移已经分配好的数据。所以流式图分割有几个优点:1)可以处理很大的图,理论上只要集群可以容纳,那么就可以处理多大的图。2)一般只加载一次图。3)相比于基于哈希的分配方式,可以有效的保留部分图的性质,进而提升算法性能。
图分割类型
图的分割按点边不同可以分成点分割(vertex-cut)和边分割(edge-cut)两种。直观就是从点切开还是从边切开,从点切开那么就是同一个点可能在多个节点当中存在多份镜像/拷贝。从边切开,那么一条边就有可能存在两个分区当中。
$\rightarrow$ 点分割(侵删):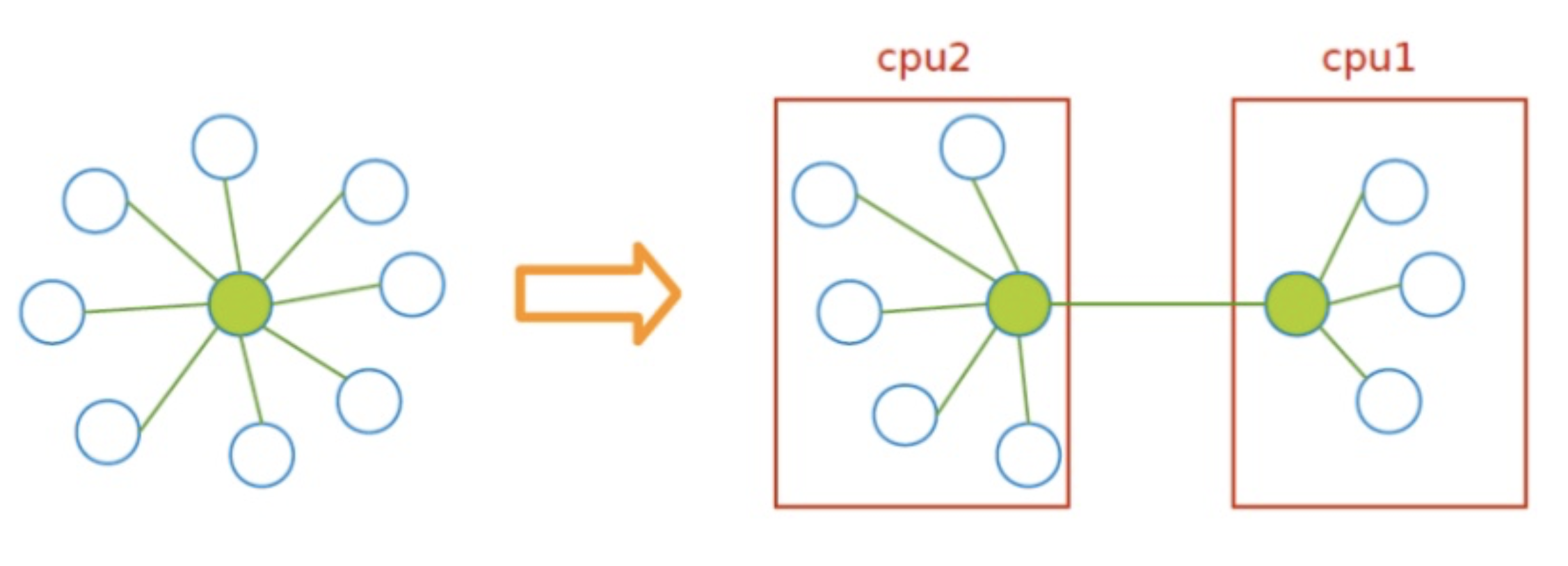
$\rightarrow$ 边分割(侵删):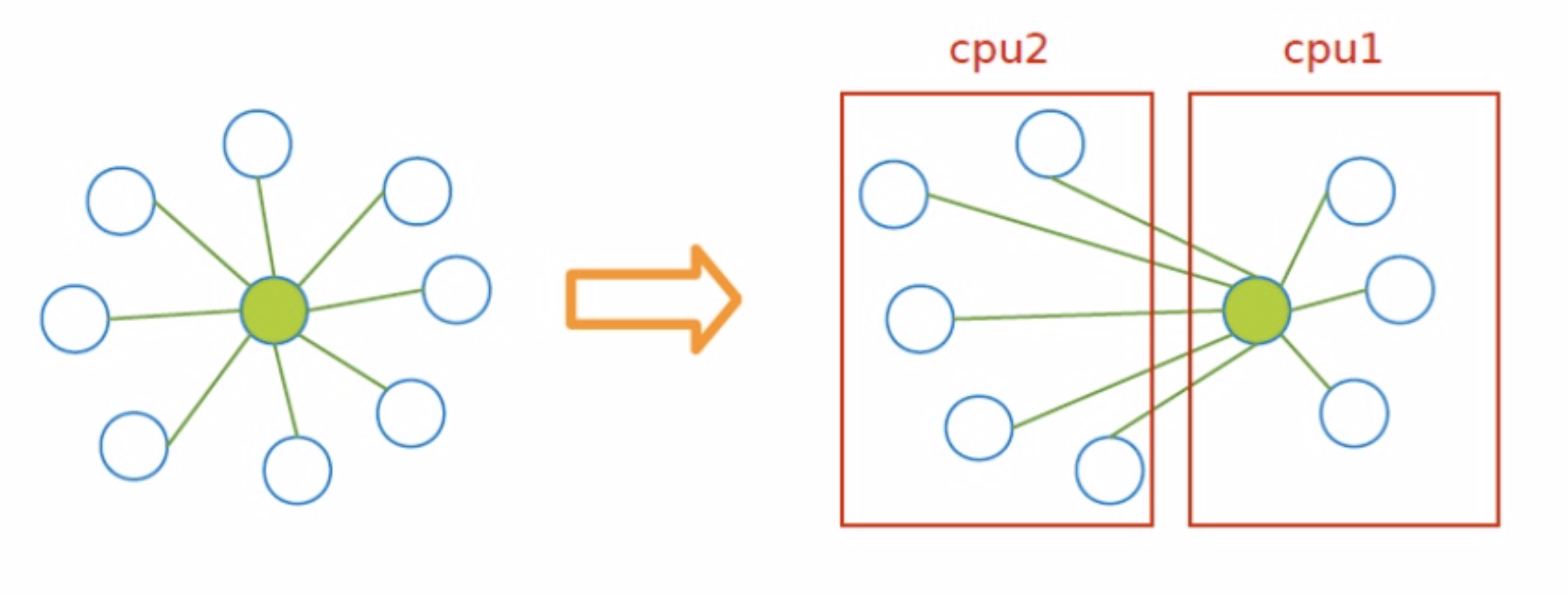
- 对于点分割来说,目标函数一般是要复制因子尽可能的小,就是不同节点中拷贝的点尽可能的少。
$$ C(P^t) = \frac{\sum\limits_{u\in V}|A(u)|}{|V|} $$
a. $A(u)$表示点$u$出现在的分区集合。$|A(u)|$表示$u$总共出现在几个分区中。
b. $P^t$表示$t$时刻的分区状态。
c. $C(P^t)$表示$P^t$当前的复制因子。
- 对于边分割来说,目标函数一般是要割(cut)尽可能的小,因为cut越小,那么一般来说通讯的代价也相应会比较小。遗憾的是Minimum k-cut的复杂度是NPC的,当图分割成k份,k是作为输入时。(注:有$O(|V|^{k^2})$复杂度的算法。wiki: Minimum k-cut)。
$$ C(P^t) = \sum\limits_{(u,v)\in E}\frac{|P^t(u)\neq P^t(v)|}{|E|} $$
a. $P^t(u)/P^t(v)$ 表示$t$时刻$u$/$v$所在的分区。($u,v$不在同一个分区内,那么$(u,v)$这条边就属于割集)
b. $P^t$表示$t$时刻的分区状态
c. $C(P^t)$表示$P^t$当前的割。
流式边分割
- KDD 2012的paper中[1],对于点$u$,作者将$u$分配到当前邻居最多的节点当中,如以下等式所示。如果$u$在节点一中有3个邻居,在节点二中有5个邻居,那么$u$会被分配到节点二当中。$C$表示每个节点最大容量。当某个分区达到容量以后,强制停止分配到当前节点(后半部分因子为0)。
$$ \arg\min\limits_{i\in{1,\ldots,k}}(|P_i^t\cap N(u)| * (1 - \frac{|P^t_i|}{C})), C=\beta \frac{|V|}{k}$$
- WSDM 2014的paper中[3],基于上述的基础,引入了不平衡因子,使得分区的大小可以在一定的范围内(不需要完全的balance)。
流式点分割
DBH[4]是改进自哈希分割。改进的地方是对于每一条边,对于度较小的顶点哈希。这样的好处是可以增强分区的局部性。
HDRF[5]是CIKM2015的一篇论文。这篇文章的score function由两部分组成,复制因子和平衡因子。
$$ C(e,P_i) = C_{REP}(e,P_i) + \lambda C_{BAL}(P_i), e=(u,v)$$
这篇文章有一个比较有意思的点是提出的score function尽可能的对度比较高的点去做镜像。
$$ C_{REP}(e,P_i) = g(u,v,P_i) + g(v,u,P_i)$$
$$ g(v, u, P_i) = 1 + \frac{deg(u)}{deg(v) + deg(u)}$$
当$v \in P_i$时,反之为0。对于$u$ $v$在同个分区当中,这个好理解我们就不提了。当$u$,$v$分属于不同分区时不妨设为$P_1$和$P_2$,那么我们肯定是把这条边放在这两个分区中的一个。这意味着要对$u$在$P_2$中做一个镜像并把$e$放在$P_2$当中,或者要对$u$在$P_1$中做一个镜像并把$e$放在$P_1$当中。由于上述提到的,我们希望对于度比较高的点做镜像。Balance的score function可以参考原文,原因是如果没有平衡因子,根据原来的score function,以及streaming的顺序,所有的点都有可能在同一个分区内。
如下图所示(侵删)
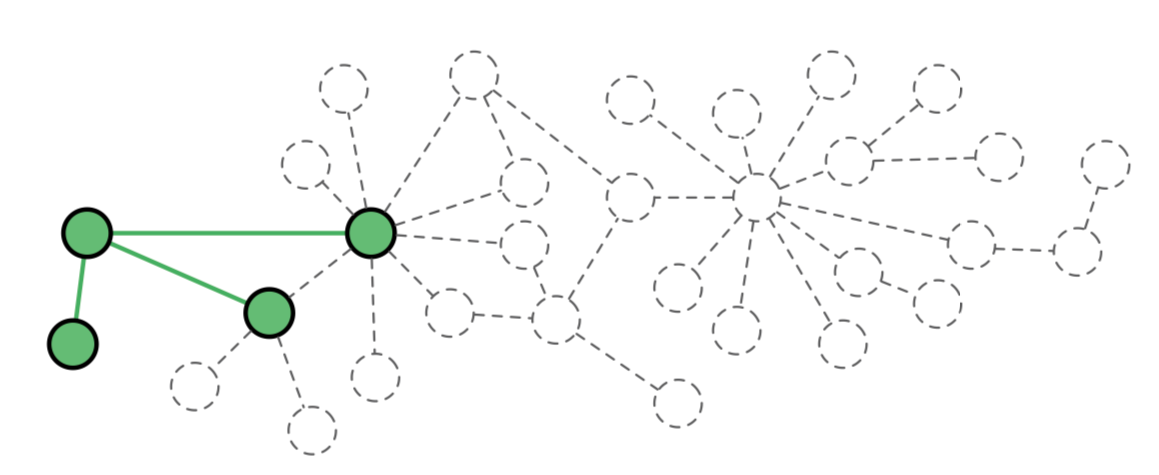
- 1.Stanton I, Kliot G. Streaming graph partitioning for large distributed graphs[C]//Proceedings of the 18th ACM SIGKDD international conference on Knowledge discovery and data mining. ACM, 2012: 1222-1230. ↩
- 2.Anil Pacaci and M. Tamer Özsu. 2019. Experimental Analysis of Streaming Algorithms for Graph Partitioning. In Proceedings of the 2019 International Conference on Management of Data (SIGMOD ‘19). ACM, New York, NY, USA, 1375-1392 ↩
- 3.Charalampos Tsourakakis, Christos Gkantsidis, Bozidar Radunovic, and Milan Vojnovic. 2014. FENNEL: Streaming Graph Partitioning for Massive Scale Graphs. In Proc. 7th ACMInt. Conf. Web Search and Data Mining. 333–342. ↩
- 4.Cong Xie, Ling Yan, Wu-Jun Li, and Zhihua Zhang. 2014. Distributed power-law graph computing: Theoretical and empirical analysis. In Advances in Neural Information Proc. Systems 27, Proc. 28th Annual Conf. on Neural Information Proc. Systems. 1673–1681 ↩
- 5.F. Petroni, L. Querzoni, K. Daudjee, S. Kamali, and G. Iacoboni. HDRF: Stream-based partitioning for power-law graphs. In CIKM, 2015. ↩
- 6.J. E. Gonzalez, Y. Low, H. Gu, D. Bickson, and C. Guestrin. PowerGraph: Distributed graph-parallel computation on natural graphs. In OSDI, pages 17–30, 2012. ↩